首先我们来看一下最常见的人工智能算法是什么样的：

人工智能算法包括几个部分：

x是模型的输入，y是模型的输出，模型就是对输入转化为输出的计算。比如输入x可以是一张图片（如猫的照片），模型对图片进行计算处理，然后输出这张图片上对应的物品的类别（猫）。

我们可以把算法理解成一个函数：y = f(x)，这里面输入是x，输出是y，模型对应的是映射规则f。

对于一个具体的问题，我们可以获取到大量的（x，y），人工智能算法就是从这些数据中学习规律，找到映射规则f。所以，人工智能算法学习规律就是确定x到y的映射规则f

为了让大家能理解人工智能算法的学习过程，我们一起来看一个简单的例子：

下面是某个小区的房价和房屋面积的数据。

现在要利用人工智能的算法去学习房屋面积和房屋价格的规律，也就是根据房屋的面积如何计算得到房屋的价格。

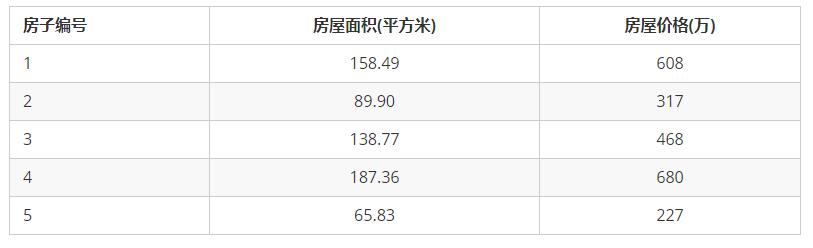
模型的输入是房屋面积，模型的输出是房屋价格。

我们可以建立这样的模型：y = wx + b

其中，w和b是未知的，调整w和b的值可以得到不同的映射规则。算法要从数据中学习，找到最优的w和b。

接下来我们一起看一下如何去确定w和b的值。

首先，我们先不管w和b取什么值，我们直接把输入代入模型，可以得到模型的输出值，我们称模型的输出为预测值。数据如下表：

接着，我们只要调整w和b的值，让预测房价尽量接近真实房价。

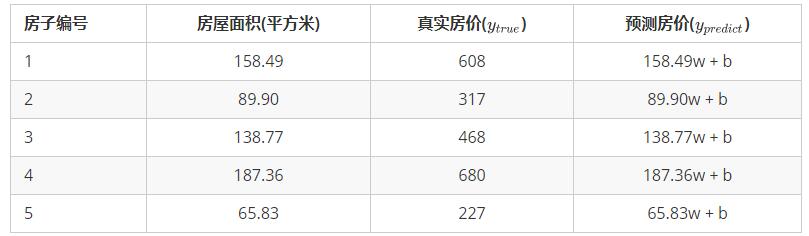
那我们怎么调整w和b呢？一个个尝试不同的取值吗？

我们知道，不管是w还是b，都是有无限种可能取值的，遍历它们的所有可能取值显然是不现实的。

那么有没有方法可以指引我们去找到最优的w和b呢？答案是有的。

回忆一下，高中数学课程里面我们是不是做过这样一件事情：给定一个函数，求函数值的最小值以及此时自变量的值。

基于这样的思路，我们做下面这样的操作：

我们用表示预测房价，用表示真实房价。我们现在来构建这样一个函数：

公式展开的结果是这样的：

这里我们就得到了一个函数，函数的自变量是w和b。大家观察这个函数，的值越小，是不是越接近？

这时候我们求这个函数的值最小的时候对应的w和b的取值，是不是就得到了我们需要找的最优的w和b的值？

答案是肯定的，人工智能算法就是这样做的。

上面我们构造的函数，在人工智能算法里面叫损失函数，求损失函数的值最小时，可训练参数(w和b)的值的方法是梯度下降。关于损失函数和梯度下降的内容，我们后面再深入去讲解。这一小节我们要理解的是人工智能算法学习的过程。

下面我们来总结一下人工智能算法学习规律的思路：

• 1、把问题抽象成数学问题：确定输入是什么，输出是什么；

• 2、建立一个模型：这个模型有很多未知的参数，参数取不同的值，模型能变成不同的映射规则；

• 3、用大量的数据去训练模型：确定各个未知参数的值，这时候模型就确定下来了。

寻找最优未知参数的值的方法：

构建一个损失函数，损失函数满足一下条件：

• 1、损失函数是关于所有可训练参数的函数；

• 2、损失函数的函数值越小，越接近。

有了损失函数之后，寻找最优可训练参数的问题就转化成：

求损失函数最小值（极小值）时，可训练参数的取值 --> 通过梯度下降法可以实现