1-问题引入

我们都参加过高考，据统计，高考的物理成绩确实与数学成绩有一定关系，但除此之外，还存在很多影响物理成绩的因素，例如：是否喜欢物理，用在物理上的时间等。而当我们主要考虑数学成绩对物理的影响时，就是要考察这两者之间的相关关系。

现实生活中还有很多的相关关系，如

1.商品销售输入与广告支出经费之间的关系，销售输入与广告支出有着密切的关系，但是还与商品质量、居民收入等因素有关。

2.粮食产量与施肥量之间的关系。在一定范围内，施肥量越大，粮食生产就越高。除此之外，粮食产量还受到土壤质量、降雨量等的影响。

3.人体内脂肪的含量与年龄之间的关系。在一定年龄段内，随着年龄的增长，人体内的脂肪含量会增加，但人体内的脂肪含量还和饮食习惯，体育锻炼有关系，可能还与先天

体质有关系。

对于上述两个变量之间的关系，应该说都可以根据经验做出相应的判断，因为“经验当中有规律”，但是，不管你经验多么丰富，如果只凭借经验办事，还是很容易出错。因此在分析两个变量之间的相关关系时，我们需要一些说服力的办法。

在寻找变量之间的相关关系中，统计同样发挥着非常重要的作用。因为上面提到的这种关系，并不像匀速直线运动中时间与速度的关系那样是完全确定的，而是带有不确定性，这就需要通过收集大量的数据（有时候通过调查、或实验），在对数据进行统计分析的基础上，发现其中的规律，才能让他们之间的关系做出判断。

2-脂肪含量和年龄相关吗？

两个变量的线性相关：

如下表中描述了人体的脂肪百分比和年龄的关系图表：

年龄脂肪含量

239.5

2717.8

3921.2

4125.9

4527.5

4926.3

5028.2

5329.6

5430.2

5631.4

5730.8

5833.5

6035.2

6134.6

问题：根据上述数据，人体的脂肪含量与年龄之间有怎么样的关系呢？

对问题的描述：

一般地，对于某个人来说，他的体内脂肪不一定随年龄增长而增加或减少，但是如果把很多个体放在一起，这时就可能表现出一定的规律性，各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均值。观察上述表数据，从大体上看，随着年龄的增加，人体中脂肪的百分比也在增加。为了确定这一细节，我们需要进行数据的分析，与以前一样，我们可以做统计图、表，通过作统计图、表，可以使我们对两个变量之间的关系有一个直观的印象和判断。

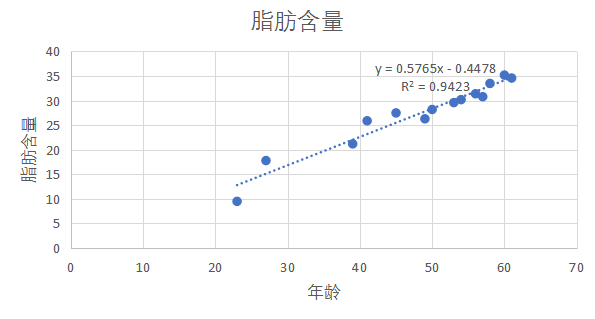
下面我们做一个散点图，如图，假设人的年龄影响体内脂肪含量，于是，按照习惯，以x轴表示年龄，y轴表示脂肪含量，得到下图：

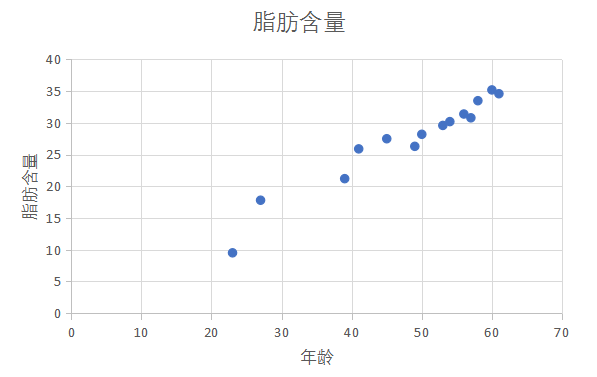
这些散分布的位置也是值得注意的，他们散布在从左上角到右下角的区域。对于两个变量的这种相关关系，我们称为正相关。还有一些变量，例如汽车的重量和汽车每消耗1L汽油所行驶的平均路程，是负相关，也就是汽车越重，每消耗1L汽油所行驶的平均路程就越短，这时的点如果绘制在画布上 将会从左上角到右下角的区域内。

接下来，需要进一步考虑的问题是，当人的年龄增加时，体内脂肪含量到底是以什么方式增加的呢？

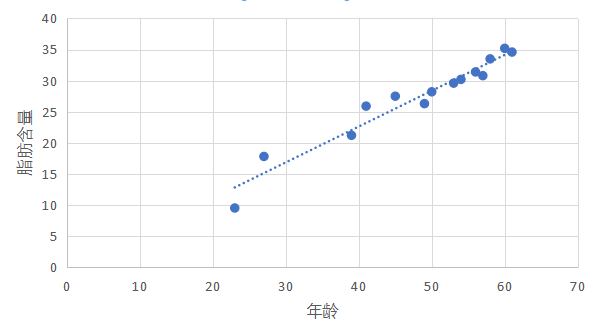
从散点图可以看出，这些点大致分布在通过散点图中心的一条直线附近，如果散点图中的点分布从整体上看大致是在一条直线附近，我们就称这两个变量之间具有线性相关关系，这条直线叫做回归直线（regression line）。

如果能求出这条回归直线的方程，那么我们就可以清晰的了解年龄与体内脂肪含量的相关性，就像平均值可以作为一个变量的数据的代表一样，这条直线可以作为两个变量具有线性相关性的代表。

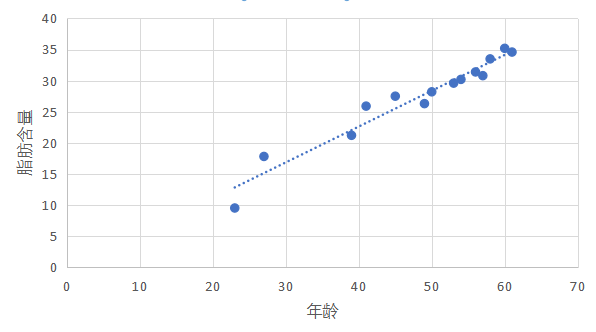
当你拿到这样一个任务的时候，你可能会采用测量的做法，先画出一条直线，测量各点与它的距离，然后移动直线，到达一个使得距离的和最小的位置，测量出此时的斜率和截距，既可以得到回归方程了。

也可能会采用平均方法，也就是在散点图中多取几组点，确定出几条直线的方程，在分别求出各条直线的斜率、截距的平均数，将这两个平均数作为回归方程的斜率和截距。

3-问题的求解

上面方法虽然有一定道理，但是总让人感觉可靠性不强。实际上，求回归方程的关键是如何用数学的方法来刻画“从整体上，各点与此直线的距离最小”。

假设我们已经得到两个具有线性相关关系的变量的一组数据

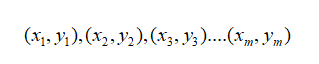
且所求的回归方程设为

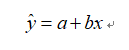
它与实际数据的偏差是

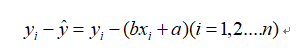
在坐标轴中表示如下

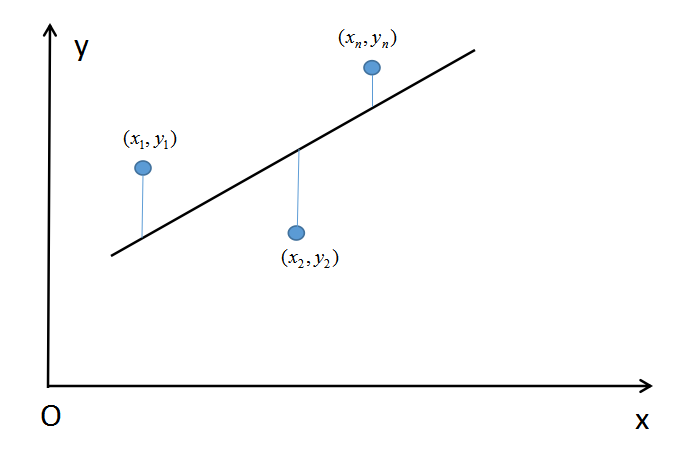
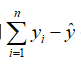这样，用这n个偏差的和来刻画“各点与此直线的整体偏差”比较合适的，由于 可正可负，为了避免互相抵消，可以考虑用代替，但由于它含有绝对这，运算不方便，所以改用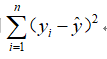

即：

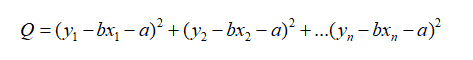
这样，问题就归结为：当a和b取什么值时Q最小，即总体偏差最小，经过数学上的最小值运算，a和b的值由下面式子给出

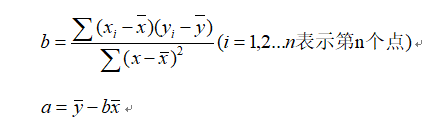
其中b是回归方程的斜率，a是截距。

总结：这种通过求解Q关系式的最小值而得到回归直线的方法，即求回归直线，使得样本数据的点到它的距离的平方和最小的方法，叫做最小二乘法（Least square）。

4-Execl绘制相关图形

Execl画回归拟合直线如下方法：

（1）准备数据，首先绘制散点图

（2）在散点图基础上点”趋势预测”即可看到拟合的直线。

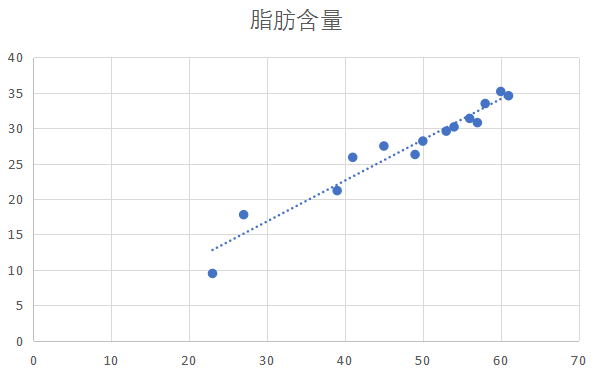
（3）在图示区域显示拟合直线的方程

5-SparkMl代码实战

这里采用基于DataFrame的SparkMl完成实验，并与Execl的结果进行对比分析：

代码部分：

import org.apache.spark.ml.linalg.Vectors

import org.apache.spark.ml.regression.{LinearRegression, LinearRegressionModel}

import org.apache.spark.sql.SparkSession

object testFat {

  def main(args: Array[String]): Unit = {

  val spark: SparkSession = SparkSession.builder().master("local[*]").appName("traintestSplitTest").getOrCreate()

    spark.sparkContext.setLogLevel("WARN")

    val data = spark.createDataFrame(Seq(

      (9.5, Vectors.dense(23)),

      (17.8, Vectors.dense(27)),

      (21.2, Vectors.dense(39)),

      (25.9, Vectors.dense(41)),

      (27.5, Vectors.dense(45)),

      (26.3, Vectors.dense(49)),

      (28.2, Vectors.dense(50)),

      (29.6, Vectors.dense(53)),

      (30.2, Vectors.dense(54)),

      (31.4, Vectors.dense(56)),

      (30.8, Vectors.dense(57)),

      (33.5, Vectors.dense(58)),

      (35.2, Vectors.dense(60)),

      (34.6, Vectors.dense(61))

    )).toDF("label", "features")

    //1-data split

    val Array(train, test): Array[Dataset[Row]] = data.randomSplit(Array(0.9, 0.1), seed = 120L)

    //2-training model

    val lr: LinearRegression = new LinearRegression()

    val lrModel: LinearRegressionModel = lr.fit(data)

    //3- Print the coefficients and intercept for linear regression

    println(s"Coefficients: ${lrModel.coefficients} Intercept: ${lrModel.intercept}")

    // 4-Summarize the model over the training set and print out some metrics

    val trainingSummary = lrModel.summary

    println(s"numIterations: ${trainingSummary.totalIterations}")

    println(s"objectiveHistory: [${trainingSummary.objectiveHistory.mkString(",")}]")

    trainingSummary.residuals.show()

    println(s"RMSE: ${trainingSummary.rootMeanSquaredError}")

    println(s"r2: ${trainingSummary.r2}")

    //    Coefficients: [0.5764772505370067] Intercept: -0.44779925795753567

    //    numIterations: 1

    //    objectiveHistory: [0.0]

    //    +---------------------------------------------+

    //    |           residuals|

    //    +--------------------------------------------+

    //    |  -3.311177504393619|

    //    |   2.682913493458356|

    //    .............................

    //    RMSE: 1.629890205389517

    //    r2: 0.9423379190667397

  }

}

这里得到的R2是回归问题的考量标准，越接近于1效果越好，这里r2为0.94效果能够达到预期，因此能够证明随着年龄的增长脂肪含量会随着增长，在回归问题中此类问题常称之为一元线性回归或简单线性回归，当然可以考虑更多的变量因素存在对脂肪含量的影响，这里不再一一列举。

6-总结

通过对脂肪含量和年龄的关系问题猜想、定义、Execl绘图分析、SparkMl建模分析得到我们猜测和数学上可证明的结论，同学们可以借助SparkMl技术解决更多的回归问题。加油！