在这篇⽂章中，我们将从头开始实现⼀个简单的3层神经⽹络。假设你熟悉基本的微积分和机器学习概念，例 如：知道什么是分类和正规化。理想情况下，您还可以了解梯度下降等优化技术的⼯作原理。

但是为什么要从头开始实施神经⽹络呢？它可以帮助我们了解神经⽹络的⼯作原理，这对于设计有效模型⾄关 重要。

1.1 ⽣成数据集 这⾥我们⾸先⽣成后⾯要⽤的数据集。⽣成数据集可以使⽤scikit-learn (http://scikit-learn.org/)⾥⾯的 make_moons (http://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_moons.html)函数

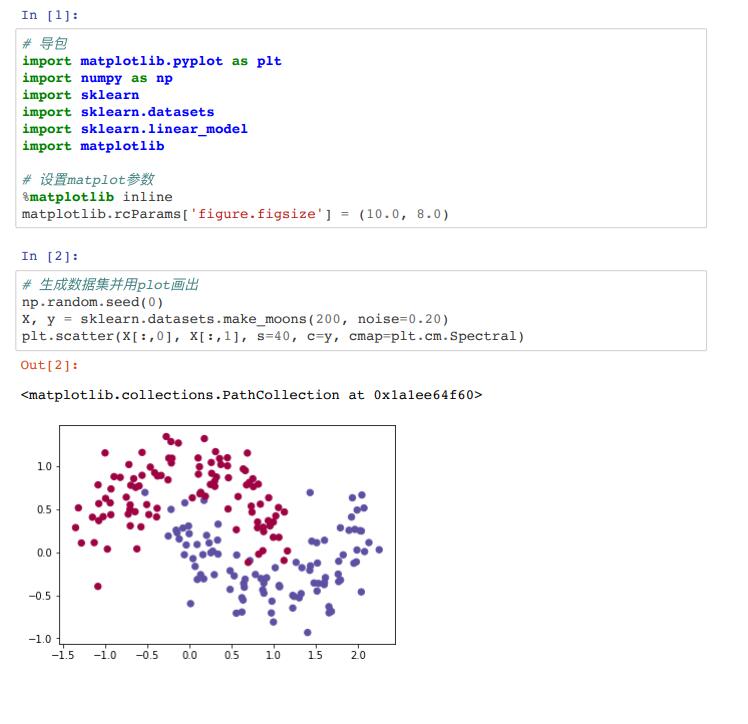
这个数据集有两个类别，分别是⽤红⾊和蓝⾊表示。我们的⽬标是使⽤机器学习的分类器根据x, y坐标预测出 正确的类别。注意这⾥的数据并不是线性可分的。我们不能画⼀条直线把这个数据集分成两个类别。这就意味 着，线性分类器，⽐如逻辑回归⽆法对我们的数据进⾏拟合，换⾔之就是⽆法⽤线性分类器对这个数据集进⾏ 分类。除⾮⼿动构造⾮线性特征，⽐如多项式。事实上这正是神经⽹络的主要优点之⼀。使⽤神经⽹络我们不 ⽤去做特征⼯程 (http://machinelearningmastery.com/discover-feature-engineering-how-to-engineerfeatures-and-how-to-get-good-at-it/)。神经⽹络的隐藏层会⾃动的学习这些特征。

1.2 逻辑回归 这⾥为了演示，我们使⽤逻辑回归进⾏分类。输⼊是数据集⾥的x, y坐标，输出是预测的类别（0或者1）。为 了⽅便我们直接使⽤ scikit-learn 中的逻辑回归

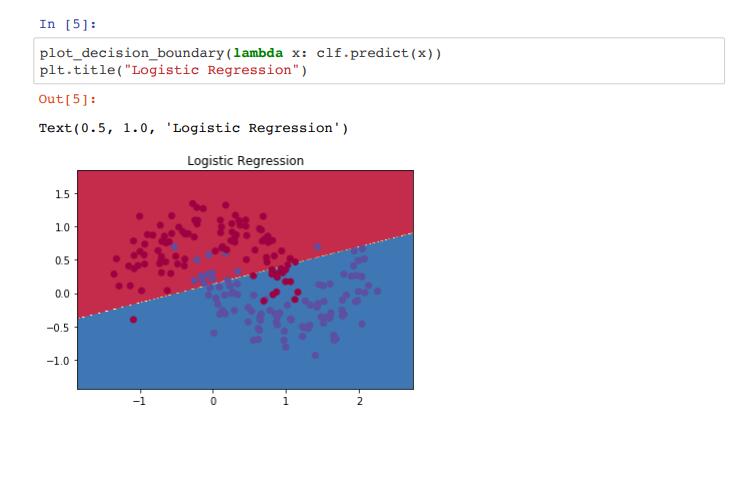
这个图显示了通过逻辑回归学习到的决策边界。这⾥的直线已经尽可能的把数据集分成两部分，但是分的效果 还是不理想，还是有些分错类别的。

1.3 训练神经⽹络

现在我们构建⼀个3层神经⽹络，其中包含⼀个输⼊层，⼀个隐藏层和⼀个输出层。输⼊层中的节点数由我们 的数据的维数确定的，这⾥是2。输出层中的节点数由我们拥有的类别数量决定，这⾥也是2。因为我们只有两 个类 实际上只⽤⼀个输出节点可以预测0或1，但是有两个可以让⽹络更容易扩展到更多的类。 ⽹络的输⼊将 是x和y坐标，其输出将是两个概率，⼀个⽤于类别0，⼀个⽤于类别1。 神经⽹络如图所示：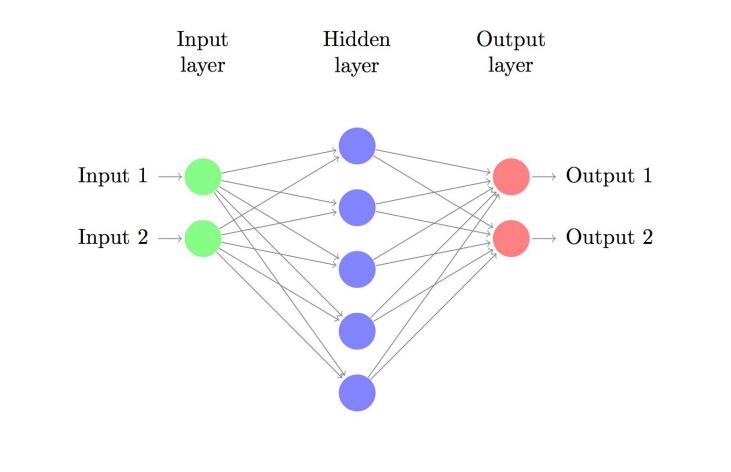

我们可以选择隐藏层的维度也就是节点数。隐藏层的节点越多，得到的神经⽹络功能就越复杂。但更⾼的维度 需要付出代价。⾸先，学习⽹络参数和预测就需要更多的计算量。同时更多参数也意味着我们得到的模型更容 易过拟合。

如何选择隐藏层的⼤⼩？虽然有⼀些指导⽅针，但实际上具体问题需要具体分析，稍后我们将改变隐藏层中的 节点数量来查看它如何影响我们的输出。

我们需要为隐藏层选择激活函数。激活功能将层中的输⼊转换为相应的输出。⾮线性激活函数允许我们拟合⾮ 线性假设。常⻅的激活函数有tanh (https://reference.wolfram.com/language/ref/Tanh.html), sigmoid (https://en.wikipedia.org/wiki/Sigmoid_function), 或者 ReLUs (https://en.wikipedia.org/wiki/Rectifier_ (neural_networks))。 这⾥我们将使⽤ tanh ，这个函数有个很好的属性就是它的导数可以使⽤本身的函数值 计算。 的导数是 。这很有⽤，这样我们只⽤计算 ⼀次，然后重新使⽤它的值来获得导 数。

因为我们希望神经⽹络最终输出概率值，所以输出层的激活函数使⽤softmax (https://en.wikipedia.org/wiki/Softmax_function)这只是将原始分数转换为概率的⼀种⽅法。同时如果熟悉逻辑 函数，可以认为softmax可以做多分

。 1.3.1 ⽹络如何做预测呢？

 我们的⽹络使⽤前向传播进⾏预测，这些只是⼀堆矩阵乘法和我们在上⾯定义的激活函数的应⽤。如果 是我 们⽹络的⼆维输⼊，那么我们按照下⾯的顺序计算得到预测 （也是⼆维的），如

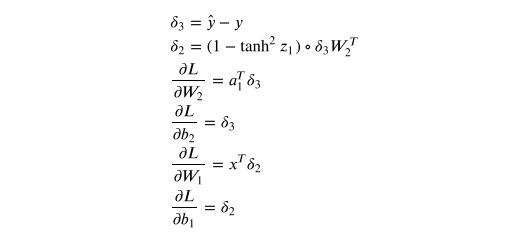
注意我们的⽬标是找到最⼩化损失函数的参数。

 我们可以使⽤梯度下降 (http://cs231n.github.io/optimization1/)来找到它的最⼩值。 我将实现最流⾏的梯度下降版本，也称为具有固定学习速率的批量梯度下降。 

诸如 SGD（随机梯度下降）或⼩批量梯度下降之类的变化通常在实践中表现更好。 decay the learning rate over time (http://cs231n.github.io/neural-networks-3/#anneal)。 

梯度下降需要我们求损失函数参数的导数： , , , 。 为了计算这些梯度，我们使⽤著名的反向传 播算法，这是⼀种从输出开始有效计算梯度的⽅法。

这⾥不会详细介绍反向传播的⼯作原理，⽹上有许多解释 的很好的⽂章这⾥ (http://colah.github.io/posts/2015-08-Backprop/)或这⾥ (http://cs231n.github.io/optimization-2/)。 

应⽤反向传播公式，得到⼀下内容：

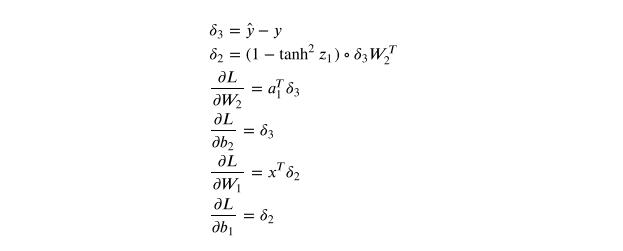
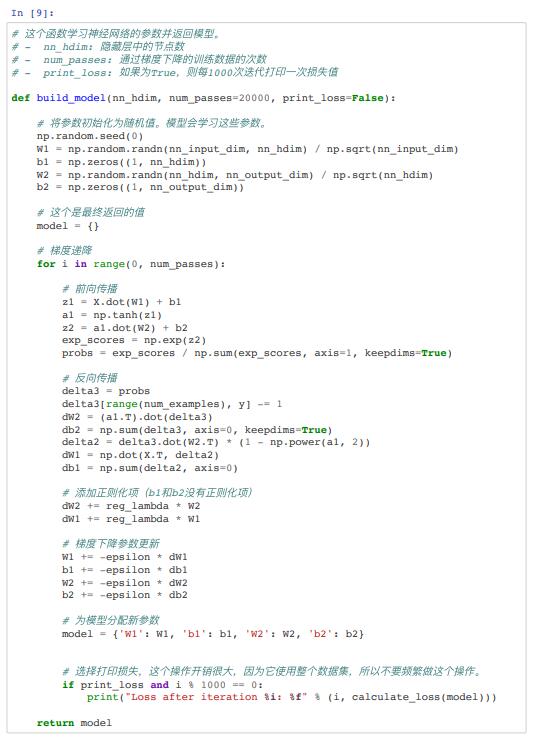
1.3.4 隐藏层⼤⼩为3的神经⽹络 

下⾯来看看如果我们训练隐藏层⼤⼩为3的⽹络会发⽣什么。

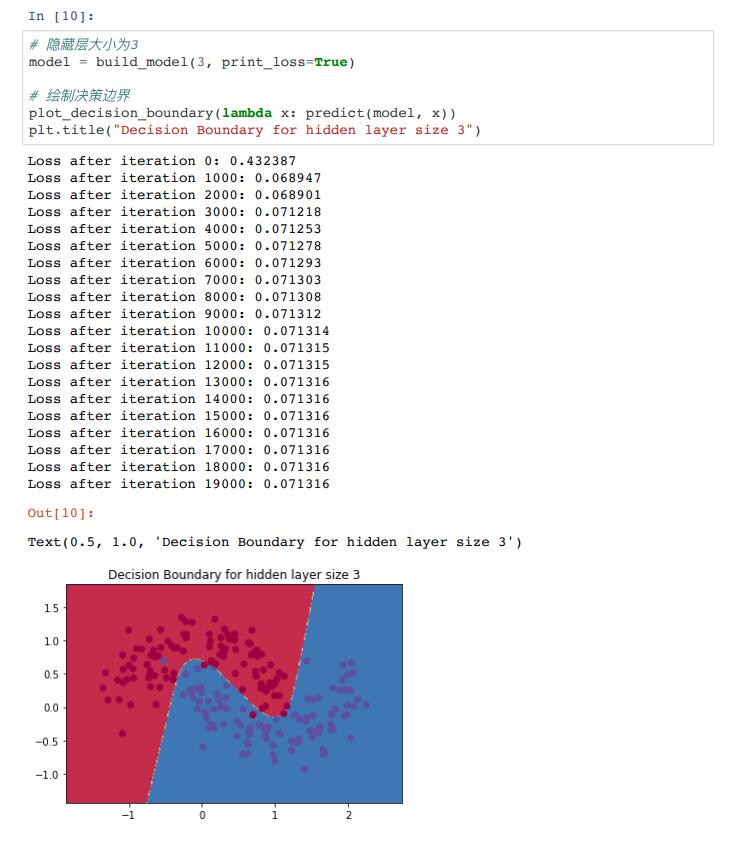
这看起来很不错。我们的神经⽹络能够找到⼀个成功分离两个类别的决策边界。

2 改变隐藏的图层⼤⼩ 

在上⾯的示例中，我们设置了隐藏层⼤⼩3，接着看看改变隐藏层⼤⼩对结果的影响。